Difference between revisions of "User:Mjb/Time-constant-based EQ"
(→CD/DAT pre-emphasis) |
(→CD/DAT pre-emphasis) |
||
| Line 60: | Line 60: | ||
</blockquote> | </blockquote> | ||
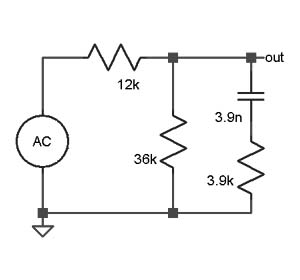
| − | Here is a circuit diagram for such a filter, from [https://www.radonmaster.de/robernd/tAFILTER.html the website of the same author]. | + | Here is a circuit diagram for such a filter, from [https://www.radonmaster.de/robernd/tAFILTER.html the website of the same author]. It has 3 resistors and 1 capacitor. Since it is passive, it reduces the overall level by about 2.5 dB, but if you boost it back up by that amount, the response is the same as shown in the plot above. |
[[File:Demp cir.jpg]] | [[File:Demp cir.jpg]] | ||
Revision as of 21:05, 24 October 2019
One thing I have always found a bit mysterious is how audio equalization filters are described in terms of "cutoff frequencies" and "time constants". Finally I think I understand it well enough, so here my attempt at explaining it to myself:
Overview
A simple, passive, "first-order" a.k.a. "one-pole" type of "lowpass" a.k.a "RC" filter consists of a resistor in series followed by a capacitor in parallel. If the components are swapped, they comprise a highpass filter. Add another resistor and reconfigure the components with the resistor & capacitor together in parallel, followed by a resistor in parallel, and you have a pre-emphasis filter (a variation of highpass) or a de-emphasis filter (a variation of lowpass). Incorporate an op-amp in to the design, and any of these will amplify the signal and then can be called active instead of passive. These are all still considered RC filters.
The time constant "τ" is R×C (resistance × capacitance) and is a way of expressing a bend in an RC filter's frequency response curve. If there is only one pole, then the time constant describes the entire curve. Well, sorta. It doesn’t tell you if it’s lowpass or highpass, or pre-emphasis or de-emphasis. But it does tell you where the curve bends.
A resistor resists the flow of electrical current. A capacitor is like a little battery or reservoir for electricity; it charges and discharges over a very short amount of time.
Given that R=V/A and C=(A×τ)/V, where V=potential in Volts, A=current in Amperes, and τ=time in seconds—or given that R=(mass×length²)∕(τ×charge²) and C=(τ²×charge²)∕(mass×length²)— the calculation of R×C results in just a time duration! It is the time required to charge or discharge the capacitor by about 63.2%. For audio frequency filtering, this time is typically expressed in microseconds (µs). A microsecond is 1∕1000th of a millisecond.
Another property of τ is that it equals 1∕(2×π×f), where f is the "pole", also called the "transition", "corner", or "cutoff" frequency. This is where the voltage and power drop by -3.0103 dB to 1∕√2. f works out to be exactly 159155∕T where T is the τ value (e.g. 70 or 120). For 70 it is ~2274 Hz, and for 120 it is ~1326 Hz.
Very roughly drawn, a Bode plot (a typical logarithmic frequency response graph) has a horizontal line at 0 dB up to this frequency (this frequency range is the "pass band"), and a 45° diagonal line beyond it (this frequency range is the "stop band"). The slope of the diagonal line shows a 6 dB drop per octave (doubling of frequency), and 20 dB per decade (10X increase in frequency). The actual curve is exponential and uses those lines as its asymptotes (the lines which the curve approaches). The curve deviates from the asymptotes by 3 dB at the corner frequency, and by 1 dB at half and at double the corner frequency.
Add another resistor–capacitor pair and you have a second-order or two-pole filter which will have a slope twice as steep (12 dB per octave or 20 dB per decade). Third order would be 18 dB∕octave or 30 dB∕decade, and so on.
A side effect of these simple filters is a phase shift, in this case meaning latency, a delay in the output. As the frequency goes up, the phase of the output gets closer to 180°. Even at the cutoff frequency, the output signal is -45° out of phase. Relatively sophisticated circuits can minimize the error. In actual music, this kind of frequency-dependent phase error can result in smearing of some transients, but otherwise is harmless; just don't mix it with the original undelayed signal!
Pre-emphasis and de-emphasis circuits are often implemented with two corner frequencies. The lower one is the normal one where the signal begins to rise (for pre-emphasis) or finishes falling (for de-emphasis). The upper one is where the slope becomes level again at the higher dB level. The RIAA vinyl LP curve has three corners!
Common corner frequencies
Some common corner frequency standards in the audio world:
- US FM radio emphasis = 75 μs → 2122 Hz
- Europe FM radio emphasis = 50 μs → 3183 Hz
- CD/DAT emphasis (rarely used) = 50 µs and 15 µs → 3183 Hz and 10610 Hz
- RIAA vinyl LP EQ = 75 μs, 318 μs, and 3180 μs → 2122 Hz, 500 Hz, and 50 Hz
- cassette or open-reel magnetic tape, 1⅞ ips normal EQ (1974+) = 120 µs → 1326 Hz
- cassette or open-reel magnetic tape, 1⅞ ips chrome/metal EQ (1970+) = 70 µs → 2274 Hz
I believe the tape standards assume 400 Hz is at 0 dB (no change from input to output). CD/DAT has 0 dB at 0 Hz. The others I think use 1000 Hz as the 0 dB reference, but I am not sure about that.
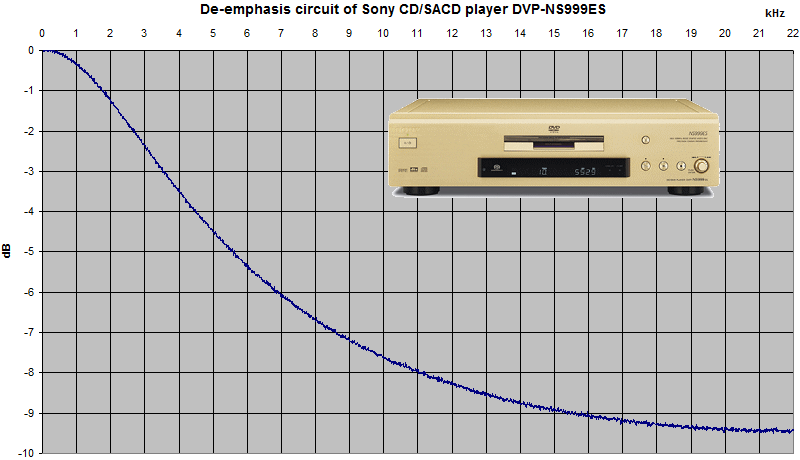
CD/DAT pre-emphasis
Here's the CD/DAT de-emphasis curve from a real CD player:
Some great info from where that was originally posted:
In a nutshell: to generate the correct target 15/50µs EIAJ de-emphasis (or pre-emphasis) curve for CD/DAT use the following equation:
- DE(f) = 10 × log(A∕B) - 10.4576
- PRE(f) = 10 × log(B∕A) - 0.9684
DE(f) is the de-emphasis output in dB at a frequency of f Hz.
PRE(f) is the pre-emphasis output in dB at a frequency of f Hz.Where:
- f = frequency in Hz
- A = 1 + ⅟(H × H)
- B = 1 + ⅟(L × L)
- H = (2 × π × f × tH)
- L = (2 × π × f × tL)
- tH = high freq. time-const (15 µs = 0.000015)
- tL = low freq. time-const (50 µs = 0.000050)
Here is a circuit diagram for such a filter, from the website of the same author. It has 3 resistors and 1 capacitor. Since it is passive, it reduces the overall level by about 2.5 dB, but if you boost it back up by that amount, the response is the same as shown in the plot above.
Cassette EQ
Magnetic tape EQ is complicated.
Much like how magnetic (MC or MM) phono cartridges are "velocity" devices, so too is a tape playback head. This means that when the tape moves past the playback head, it induces a current which results in a signal with extremely weak bass and greatly exaggerated treble. A flat signal on the tape, when played by an ideal head, produces an increasing slope of 6 dB per octave across the spectrum. This is corrected by applying a -6 dB/octave EQ in the playback amp.
Getting a flat signal onto a relatively slow-moving (1⅞ ips) cassette tape is not easy, though; there are massive treble losses during both recording and playback. The highest reel-to-reel tape speeds (30 ips) do not have this problem, so they require very little additional equalization, but the slower speeds run into physical limitations of the system. Tape formulations also affect the treble response of the tape itself; Type I has weaker treble response.
The actual signal on the tape does not need to be flat, anyway. Just like with vinyl records, there is plenty of room to exaggerate the higher frequencies during recording, and reduce them back down to normal during playback. This has the effect of keeping the signal flat yet cuts down on the HF background noise added by the medium, thus improving SNR. The NAB and IEC came up with EQ standards for EQing tape this way, concentrating on the playback side, and making it so that tapes recorded on different decks would not have extreme differences in sound quality. So, tape is expected to contain greatly exaggerated treble and slightly exaggerated bass, all of which is then corrected to be pretty close to flat during playback.
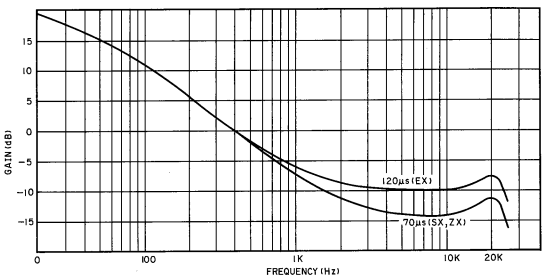
- Playback EQ consists of -6 dB/octave, plus a standard 50µs lowpass, plus an optional 3180µs highpass (proposed in 1976 but not widely adopted), plus a 120µs or 70µs lowpass depending on the cassette type. The 0 dB reference point is at 400 Hz. Here is the playback EQ for my Nakamichi deck (SX & ZX are Nakamichi's names for Type II and Type IV, respectively; and the 0 Hz mark is supposed to say 20):
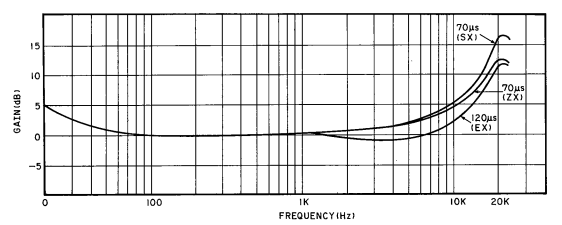
- Record EQ is expected to be whatever it takes for a particular deck to produce flat output for the playback EQ. So this always consists of a mild bass boost and a strong treble boost, plus additional EQ tuned to the individual deck. It also includes a 120µs or 70µs adjustment selected via a cassette shell notch sensor or a manual switch. Other than that sensor or switch, most decks do not allow a way to customize the record EQ without adjusting pots on the circuit board. Here is the record EQ for my Nakamichi deck (SX & ZX are Nakamichi's names for Type II and Type IV, respectively; and the 0 Hz mark is supposed to say 20):
Here is the "flux" (EQ of the recorded signal) which actually ends up on the tape (see the brown and yellow lines):
Visualizing all of this is difficult enough. It is even harder to understand why using 70µs EQ to play a tape recorded with 120µs EQ results in duller sound, when a 70µs rolloff instead of 120µs should result in brighter treble. It is also quite a mind-bender to consider that chrome & metal tapes inherently have lower noise and higher treble response, yet the treble is still boosted and cut more than for normal tapes. I have to admit that after researching this for several days, I still haven't found any explanations that put all of this together in a way I fully understand.
Although I don't really get it, the main thing is that recording with 120µs EQ results in a certain amount of treble pre-emphasis, and recording with 70µs EQ results in even more. Likewise, playback with 70µs EQ results in the inverse effect, rolling off the treble moreso than playback with 120µs EQ.
References
Some references I used:
- https://www.electronicshub.org/passive-low-pass-rc-filters/
- https://books.google.com/books?id=Ma1dAQAAQBAJ&lpg=PA90&ots=fuXWw7EX-N&pg=PA90#v=onepage&q&f=false
- http://www.sengpielaudio.com/calculator-RCpad.htm
- http://www.sengpielaudio.com/ZeitkonstanteUndUebergangsfrequenz.pdf
- https://www.gammaelectronics.xyz/audio_06-1985_eq.html (the best of Herman Burstein's redundant articles on this topic)
- http://www.richardhess.com/tape/history/NAB/NAB_Reel_Tape_Standard_1965_searchable.pdf
- http://nomanlab.com/sale/lim_docs/nab_to_ccir.pdf
- http://www.sengpielaudio.com/ZeitkonstanteUndUebergangsfrequenz.pdf
- http://mrltapes.com/equaliz.html
- http://richardhess.com/notes/formats/magnetic-media/magnetic-tapes/analog-audio/equalization/
- https://www.iasa-web.org/tc04/magnetic-tapes-replay-equalisation
- http://www.mrltapes.com/mcknight_freq-resp-of-mag-recorders.pdf